時間:2017-05-01 來源:互聯網 瀏覽量:
本文作者為Jahnavi Mahanta,前American Express(美國運通公司)資深機器學習工程師、深度學習在線教育網站Deeplearningtrack聯合創始人。
Jahnavi Mahanta:對算法的作用建立直覺性的理解——在我剛入門機器學習的時候,這讓我覺得非常困難。不僅僅是因為理解數學理論和符號本身不容易,也因為它很無聊。我到線上教程裏找辦法,但裏麵隻有公式或高級別的解釋,在大多數情況下並不會深入細節。
就在那時,一名數據科學同事介紹給我一個新辦法——用Excel表格來實現算法,該方法讓我拍案叫絕。後來,不論是任何算法,我會試著小規模地在 Excel 上學習它——相信我,對於提升你對該算法的理解、完全領會它的數學美感,這個法子簡直是奇跡。
案例
讓我用一個例子向各位解釋。
大多數數據科學算法是優化問題。而這方麵最常使用的算法是梯度下降。
或許梯度下降聽起來很玄,但讀完這篇文章之後,你對它的感覺大概會改變。
這裏用住宅價格預測問題作為例子。
現在,有了曆史住宅數據,我們需要創建一個模型,給定一個新住宅的麵積能預測其價格。

任務:對於一個新房子,給定麵積X,價格Y是多少?
讓我們從繪製曆史住宅數據開始。
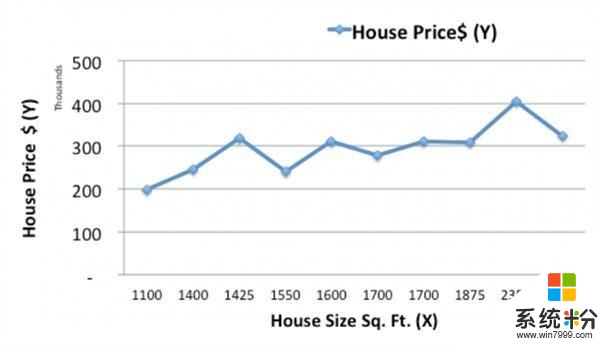
現在,我們會用一個簡單的線性模型,用一條線來匹配曆史數據,根據麵積X來預測新住宅的價格Ypred。
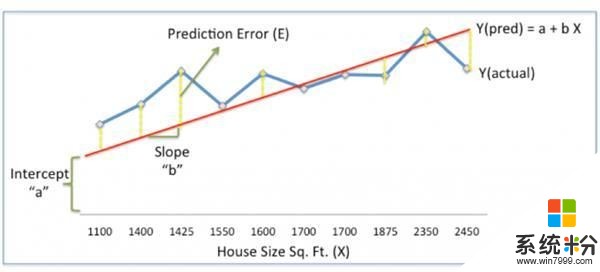
上圖中,紅線給出了不同麵積下的預測價格Ypred。
Ypred = a+bX
藍線是來自曆史數據的實際住宅價格Yactual。
Yactual和Ypred之間的差距,即黃色虛線,是預測誤差 E。
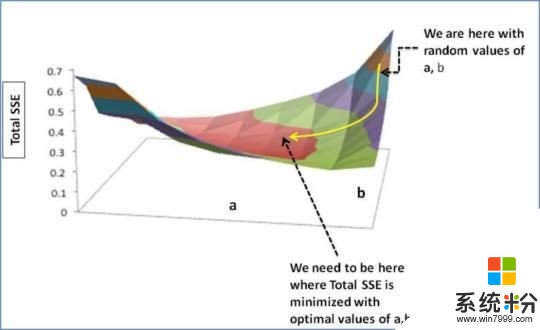
我們需要發現一條使權重a,b獲得最優值的直線,通過降低預測誤差、提高預測精度,實現對曆史數據的最佳匹配。
所以,目標是找到最優a, b,使Yactual和Ypred之間的誤差E最小化。
誤差的平方和(SSE) = ? a (實際價格 – 預測價格)2= ? a(Y – Ypred)2
(提醒,請注意衡量誤差的方法不止一種,這隻是其中一個)
這時便是梯度下降登場的時候。梯度下降是一種優化算法,能找到降低預測誤差的最優權重 (a,b) 。
理解梯度下降
現在,我們一步步來理解梯度下降算法:
用隨機值和計算誤差(SSE)初始化權重a和b。
計算梯度,即當權重(a & b)從隨機初始值發生小幅增減時,SSE的變動。這幫助我們把a & b的值,向著最小化SSE的方向移動。
用梯度調整權重,達到最優值,使SSE最小化。
使用新權重來做預測,計算新SSE。
重複第二、第三步,直到對權重的調整不再能有效降低誤差。
我在 Excel 上進行了上述每一步,但在查看之前,我們首先要把數據標準化,因為這讓優化過程更快。
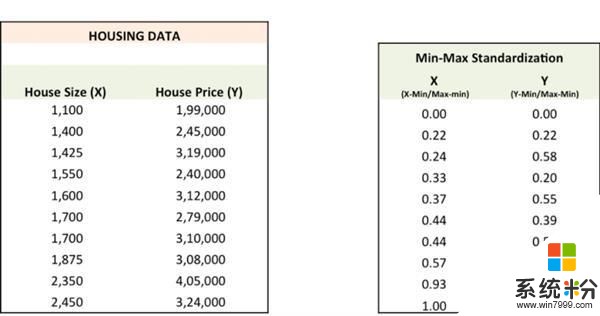
第一步
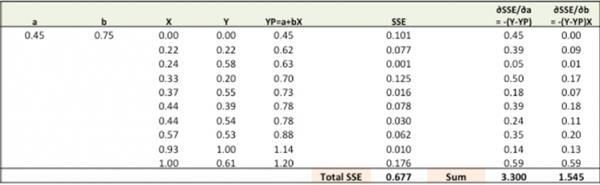
用隨機值的a、b初始化直線Ypred = a + b X,計算預測誤差SSE。
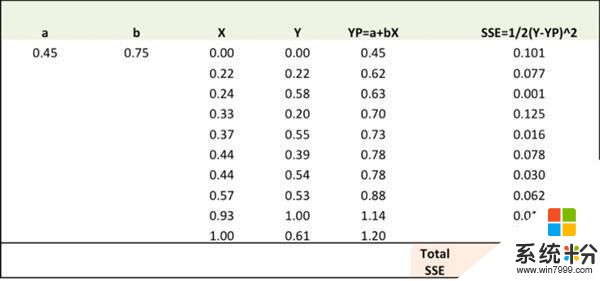
第二步
計算不同權重的誤差梯度。
?SSE/?a = – (Y-YP)
?SSE/?b = – (Y-YP)X
這裏, SSE=? (Y-YP)2 = ?(Y-(a+bX))2
你需要懂一點微積分,但沒有別的要求了。
?SSE/?a、?SSE/?b是梯度,它們基於SSE給出 a、b 移動的方向。
第三步
用梯度調整權重,達到最小化SSE的最優值
我們需要更新a、b的隨機值,來讓我們朝著最優a、b的方向移動。
更新規則:
a – ?SSE/?a
b – ?SSE/?b
因此:
新的a = a – r * ?SSE/?a = 0.45-0.01*3.300 = 0.42
新的b = b – r * ?SSE/?b= 0.75-0.01*1.545 = 0.73
這裏,r是學習率= 0.01, 是權重調整的速率。
第四步
使用新的a、b做預測,計算總的SSE。
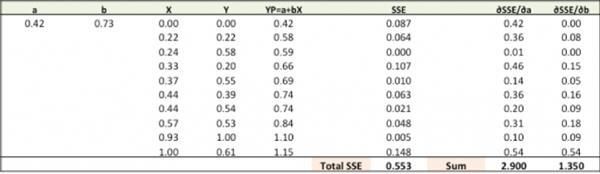
你可以看到,在新預測上 總的SSE從0.677降到了0.553。這意味著預測精度在提升。
第五步
重複第三、第四步直到對 a、b 的調整無法有效降低誤差。這時,我們已經達到了最優 a、b,以及最高的預測精度。
這便是梯度下降算法。該優化算法以及它的變種是許多機器學習算法的核心,比如深度網絡甚至是深度學習。