時間:2017-07-19 來源:互聯網 瀏覽量:
接著我們上一篇繼續,沒看前一篇的同學可以看我以前發布的文章 “「量學堂-15」假設檢驗(上)”。
讓我們先獲取股價數據:
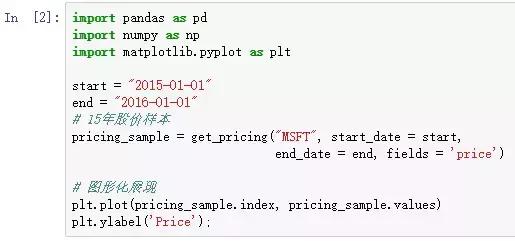
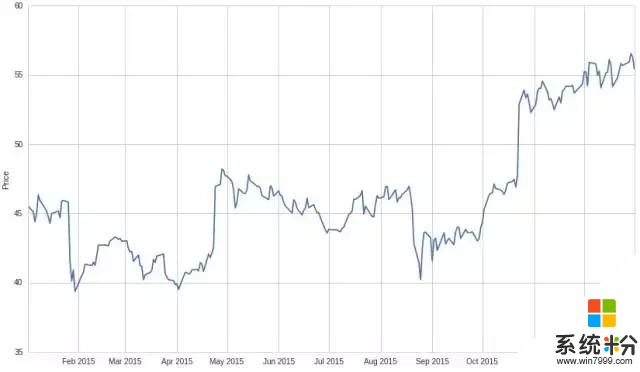
將其轉換為日收益率:

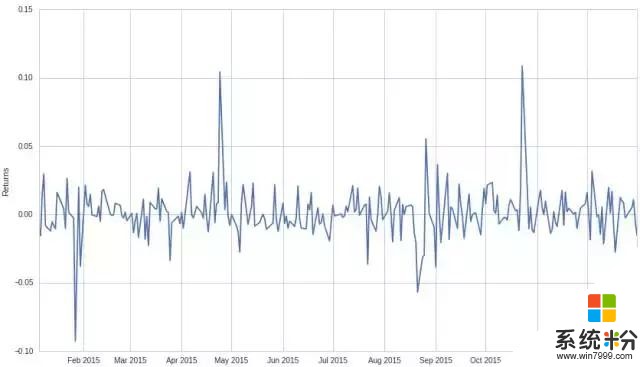
這裏不知大家是否有這樣的疑問,既然我們的“原假設(虛無假設)”與“替代假設”分別為:H0:微軟股價收益率的均值為 0;HA: 微軟股價收益率的均值不為 0。那為什麼我們不直接算得微軟的股價收益率均值,從而來直接檢驗假設的正確性呢?
因為我們無法獲得完整的總體數據(每天都會產生新的股價,生生不息),而是隻能獲得某個有限時間段內的收益率樣本。我們並不確定樣本是否可以反應總體的情況。正是由於這種不確定性,我們才需要使用統計檢驗。
下麵,我們選擇合適的檢驗統計量以及對應的概率分布。檢驗統計量通常采用以下的形式:

檢驗統計量依靠樣本數據計算出來,再與它的概率分布進行對比,來決定拒絕還是接受原假設。由於我們要檢驗的是微軟股票的平均收益率是否為0,我們可以使用樣本均值
作樣本統計量。在已知總體標準差
時,通過
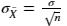
計算樣本統計量的標準差;若總體標準差未知時, 通過
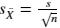
計算樣本統計量的標準差,這裏的 s 是樣本標準差。根據假設,分子“基於原假設的總體參數值”指的就是“微軟股價均值為0”,因此我們的檢驗統計量的計算公式可轉化為:
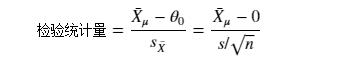
下麵是四個最常用檢驗統計量及其分布:
t-分布 (t-檢驗)
正態分布 (z-檢驗)
卡方分布 (卡方-檢驗)
F-分布 (F-檢驗)
之後我們會具體展開。就目前而言,我們嚐試在微軟的例子中應用 z-檢驗。
選定了合適的檢驗統計量以及概率分布後,我們需要指定檢驗的顯著性水平 α 值,拿它與我們的檢驗統計量比較,從而決定是接收還是拒絕原假設H0。
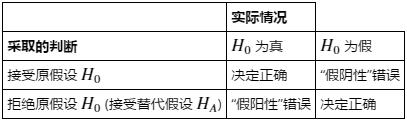
我們的顯著性水平 α =“假陽性”錯誤發生的概率(“假陽性”是指:錯誤地判斷H0不成立,實際H0 為真)。另一方麵,我們把“假陰性”錯誤發生的概率記作 β (錯誤地判斷 H0 成立,實際 H0 為假)。
如果我們試著減少“假陽性”錯誤發生的概率,我們將會增加“假陰性”錯誤發生的概率,反之亦然。同時減少兩種錯誤發生的概率的唯一方式,就是增加樣本容量。
常用的顯著性水平 α 值有:0.1, 0.05 和 0.01。若 α = 0.1 的情況下拒絕原假設(虛無假設),意味著我們有某種證據顯示原假設是錯誤的。若 α =0.05 時拒絕原假設(虛無假設),說明我們有充分的證據顯示原假設是錯誤的,而當 α =0.01 時拒絕原假設,說明我們有著極其充分的證據顯示原假設是錯誤的。
臨界值
現在我們來尋找臨界值,又稱為“拒絕臨界點”。我們將檢驗統計量與臨界值進行比較,從而決定是否拒絕原假設。如果我們拒絕,我們稱這種情況為“統計上是顯著的”,如果我們不能拒絕原假設,則稱之為“統計上不顯著”。
我們根據假設檢驗的顯著性水平阿爾法及其分布來決定檢驗臨界值 ,在本例中,假設 α = 0.05,則我們的顯著性水平就是 0.05。有兩種設定臨界值的方式來應用單邊 z-檢驗:
如果我們檢驗 H0: θ ≤ θ0,HA: θ > θ0,顯著性水平 α = 0.05,我們根據臨界值0.05查對應的Z分布表得到 z0.05 = 1.645。再將檢驗統計量 z' 與 z0.05 比較,如果 z' > 1.645,我們拒絕原假設。
如果我們檢驗的是 H0: θ ≥ θ0,HA: θ < θ0 ,顯著性水平 α = 0.05,我們同樣查對應的Z分布表得到臨界值 -z0.05 = -1.645。如果 z' < -1.645,我們將會拒絕原假設。
應用雙邊檢測則會有些許不同。由於是“雙邊”,因此將有兩個臨界點,正值和負值。我們的 α = 0.05,因此假陽性發生的概率之和要是0.05,對於雙邊檢驗的情況,我們將 0.05分成“一半一半”,我們將正、負臨界點分別記作 z0.025 和 -z0.025,對照分布表得到臨界值分別為 1.96 和 -1.96。這種情況下,如果 z' < -1.96 或者 z' > 1.96,我們就拒絕原假設。而如果 -1.96≤ z' ≤ 1.96,我們則接受原假設。
當進行假設檢驗的時候,你也可以使用 P-值 來進行判斷。P-值 是你可以拒絕原假設的最小顯著性水平。人們經常把 P-值 理解成“原假設是錯誤”的概率,這是一種誤解。P-值 隻有在與顯著性水平比較時才有意義。如果 P-值 < α ,我們將拒絕原假設,否則我們接受原假設。注意:更小的 P-值 並非意味著統計意義上更顯著。有許多統計工具能夠為你計算P-值,當然你也可以手工計算。計算規則取決於你的假設檢驗類型以及累計密度函數。如果要手工計算P-值,應遵循下述方法:
*對於“≤”的假設檢驗,P-值 = 1-累積密度值(檢驗統計量)
*對於“≥”的假設檢驗,P-值 = 累計密度值(檢驗統計量)
*對於“≠”的假設檢驗,P-值 = 2 * (1 - 累計密度值) (檢驗統計量)
未完待續